A couple of months ago, Michigan State set an NCAA Division I-A football record for the greatest deficit overcome (35 points), in a game against Northwestern.

Tonight, Texas Tech reeled off an amazing comeback of its own, overcoming a 31-point deficit (38-7) to stun Minnesota 44-41 in overtime in the Tempe, Arizona-based Insight Bowl. The Red Raiders' rally set a bowl record for comebacks.

Interestingly, Michigan State and Texas Tech started their respective comebacks with similar amounts of time remaining. Northwestern scored on MSU to take a 38-3 lead with 9:54 left in the third quarter, whereas Minnesota went up 38-7 over TTU with 7:47 remaining in the third. It really looked like the Gophers had burrowed too deep a hole for the Red Raiders to climb out of.

One possible way to approach the Texas Tech comeback statistically is via the runs test. If we looked at the temporal sequence of the teams' scoring drives (whether for a touchdown or field goal) in regulation, it would look like this (M = Minnesota, T = Texas Tech):

M M M M T M M T T T T T

As can be seen from the color scheme, there were four "runs" in the sequence (a run being a stretch of one team scoring points without interruption by the other team). The fewer the runs, the more streakiness is present. I tested the Minnesota-Texas Tech sequence using an online runs-test calculator, typing in 1's instead of M's for Minnesota and 0's instead of T's for Texas Tech.

As explained in this document from North Carolina State University, the runs test determines how many runs would be expected by chance (which can then be compared to the actual number obtained), "given the proportion of the population in each of the two categories and given the sample size..."

In the Minnesota-Texas Tech analysis, there were significantly fewer runs than would be expected by chance (p < .05). One probably does not need a statistical test to be convinced that Texas Tech ended regulation play on a hot streak and Minnesota, on a cold one. Still, if you had never heard of the runs test before tonight, then the saying that, "You learn something every day," holds true, at least for tonight.

Every so often, one hears a reference to a coach or manager making a decision according to "the book," as though a definitive catalog of strategy for a given sport existed. Now, however, a trio of baseball authors has come along and written a volume entitled, appropriately enough, The Book, and they have a website to go with it.

The website has a blog component, whose topics include streakiness. It is through this blog that I learned about an online discussion on another board, where a contributor with the moniker "Dackle2" presented some statistics on what happens after baseball teams go through a particularly hot or cold 10-game stretch.

What looks like around 300,000 10-game sequences in Major League Baseball from 1871-2005 were extracted and classified according to teams' records during the stretch (i.e., from 0-10, 1-9, and 2-8 all the way through to 8-2, 9-1, and 10-0). Teams' winning percentages from the five games before and five games after the 10-game stretch were also noted.

If there were anything to the idea of momentum or carryover of streakiness, one would predict, for example, that after languishing through a 0-10 cold streak, teams would have an appreciably worse winning percentage in the five games after the 10-game losing streak than in the five games before. Five games, by themselves, do not constitute a great sample, but aggregating many five-game sequences over many teams and many years, the data would seem sufficient.

As seen in the linked document, however, teams did not play markedly worse immediately after their 0-10 stretches (.347) than they did immediately before them (.358). At the other extreme, teams that achieved 10-0 hot streaks did not play substantially better immediately afterwards (.620) than beforehand (.610). In fact, whichever 10-game breakdown you look at (e.g., 2-8, 5-5, 7-3), the average winning percentages for the five games before and five games after are virtually identical.

Like other studies going all the way back to the original "hot hand" research by Gilovich, Vallone, and Tversky in 1985, the present findings suggest that players and teams have characteristic baseline rates of success, and that short-term hot streaks do not lead to long-term success rates above baseline, nor do short-term cold streaks lead to long-term success rates below baseline.

One of the more interesting forms of streakiness, in my view, is seeing one team go on a run to build up a big lead, only to see the other team turn the tables and make its own spurt to come back and win the game, or at least make it close.

Last night alone in the NBA, there were at least four games that followed the above storyline:

Phoenix built a 47-22 lead over Golden State in the second quarter, only to see the Warriors rebound for an 80-72 lead (a 33-point turnaround from -25 to +8 on Golden State's part). Unfazed by blowing their huge lead, however, the Suns came back to win the game, their 13th straight victory.

Philly shaved a 17-point Dallas lead to just 3, although the Mavs pulled away again. It was the Sixers' 10th straight loss; Dallas had a 12-game winning streak earlier this season.

Sacramento erased a 16-point deficit to edge Utah.

Finally, in the late West Coast game, the Lakers came back from 21 behind to beat the Rockets.

A week ago, the Nets darted out to an 18-0 lead, but fell to Boston.

This recent lead-blowing even appears to transcend any particular sport. In NHL action last Monday, Washington squandered a 4-0 lead in falling to Pittsburgh 5-4.

The above scenarios were all that I planned to write about. But right now, upon checking the score of the Texas Tech-Arkansas men's basketball game, I see where the Red Raiders have jumped out to an 18-3 lead. Tech, to this point, has missed only one shot, whereas Arkansas has made only one. If the aforementioned games are any lesson, expect a Razorback run to get back into the game.

Update: Arkansas never got closer than eight, with Texas Tech then pulling away to win by 15.

Time to check in again on the three-point shooting of the Texas Tech men's basketball team. As noted in my November 30 posting (see below or in November 2006 archives), the Red Raiders were leading the nation in shooting percentage behind the arc, at 50.4. Citing the statistical concepts of extremity of outcomes in small sample sizes and regression to the mean, I predicted the team would drop off some.

It should also be noted that, over the past five seasons, none of the teams that led the nation in three-point percentage exceeded 44%.

2002 Oregon 42.4
2003 Illinois St. 44.0
2004 Birm. Southern 43.0
2005 Oklahoma St. 42.1
2006 Southern Utah 42.9

Since my last posting on this topic, Texas Tech has experienced a small drop in its accuracy from long distance, sitting currently in second place nationally at 47.8.

In the Red Raiders' three most recent games (season log), they had two poor outings from three-point land (4-14, .286 vs. Stanford, and 2-10, .200 vs. Louisiana Tech), followed by an 11-18 (.611) explosion vs. Centenary. I was at the Centenary game and noticed some fans marking each of Texas Tech's made treys by unveiling a succession of cloth signs with 3's on them. With the help of my faculty colleague Bo Cleveland (with later technical assistance by Rachna Mutreja), we were able to take the following photo of the display in full glory at game's end.





I'll continue to track the story. It's important to state that, even if Texas Tech's three-point percentage continues to drop -- as I predict it will -- the team could still lead the nation, as other teams will likely drop too. In other words, Texas Tech's anticipated drop would be in absolute terms, but not necessarily in relative terms.

In terms of individual players, BYU's Austin (Got the Range) Ainge is now down from his earlier 70.6 three-point percentage (which I cited in my previous write-up) to 54.2.

It was just a few days ago (see November 30 posting below) that I talked about how extreme patterns can occur when looking at a small number of observations (e.g., several batters hitting above .400 early in the baseball season). But, I warned, it's hard to maintain extremely high (or low) levels of performance over larger numbers of attempts.

Yesterday, however, a Division III men's basketball player did as much as can be done within a single game to contradict my assertions. What happened was that Lincoln University's Sami Wylie shot 51% on three-pointers.

If a player were to have shot (roughly) 50% on 10 three-point attempts, I would find that moderately interesting. In 20 attempts? More impressive. And so on as the number of shots from behind the arc increased.

Well, in Wylie's case, he shot 51% on 41 attempts from three-point land. Yes, he shot 41 times from downtown, making 21 treys! All told, he ended up with 69 points in Lincoln's 201-78 win over Ohio State-Marion.

ESPN.com's article likens the game to a scene from the movie Pleasantville, where "every shot from every conceivable angle goes in."

First, a disclosure: I received my undergraduate degree at UCLA, in 1984.

Going into this year's annual USC-UCLA football game, played earlier today, the rivalry over the past 15 years had been as streaky as is possible for a situation where both teams had enjoyed stretches of dominance.

1991 UCLA
1992 UCLA
1993 UCLA
1994 UCLA
1995 UCLA
1996 UCLA
1997 UCLA
1998 UCLA
1999 USC
2000 USC
2001 USC
2002 USC
2003 USC
2004 USC
2005 USC

With UCLA's eight straight wins, followed by USC's seven, we don't need a statistical test to tell us that the number of observed runs (uninterrupted streaks by one team) is the minimum possible -- two -- given that each team has won at least once.

USC was widely expected to beat UCLA today en route to the (mythical) national championship game, in the process tying UCLA's earlier eight-game winning streak in the Battle of Los Angeles.

But it wasn't to be. UCLA 13, USC 9.

Being a faculty member at Texas Tech University, I periodically check out the Internet discussion boards related to the school's sports teams. It was there that I learned a few hours ago that the Red Raider men's basketball team is, at the moment, leading the NCAA in three-point shooting percentage.

Texas Tech has made 58 of 115 attempts from behind the arc (50.4%). While I was looking at the team statistics, I decided to peruse the individual three-point shooting statistics, as well.

Excluding three players who are each 2-for-2 (100%) on three-pointers due to insufficient attempts, the current national leader among individuals is BYU's Austin Ainge, who's hit 12-17 (70.6%). (For those who are wondering, Austin is indeed the son of former NBA guard Danny.) I guess you can say the young Ainge has the range!

Neither Texas Tech's 50% success rate as a team, nor Ainge's 70% rate, is likely to hold up for the season. Last year's three-point percentage leaders at the end of the season were Southern Utah (team) at 42.9% and Northern Arizona's Stephen Sir (individual) at 48.9%.

The current season is about one-fourth of the way through. What we're likely seeing, therefore, is the extremity of results associated with small numbers of observations. This concept was first brought to my attention by Geoff Fong in the spring of 1984, when he was on the faculty at Northwestern and I was visiting during my tour of prospective graduate schools (I ultimately chose Michigan).

Geoff was telling me about his research on statistical reasoning, and he pointed out how, early in every Major League Baseball season, the list of batting leaders will tend to have several players hitting above .400, yet there would be virtually no chance of any player ending the season at that level (the last player to hit .400 or better for a season was, of course, Ted Williams in 1941).

This statistical document describes the small-numbers phenomenon a bit more technically:

...all other things being equal, variation is more pronounced with small samples than with large ones. The larger your sample, the more stable your results will be. They will be less subject to the possibility that another study would produce greatly different results. A corollary is that large samples are less likely to produce extreme results. For example, assuming that you have a fair coin, it's much more difficult to get all heads when you toss a coin 50 times than when you toss it only two or three times.

Let's use last year's Texas Tech three-point success rate of .390 as a baseline for this year's squad (though there has been some change in personnel, most of the Red Raiders' outside shooters are still on the team, including offensive stalwart Jarrius [Jay] Jackson).

Using an online calculator for what is known as a binomial probability, we can ask how likely it is that a .390 three-point shooting team (which is what this year's Red Raiders are assumed to be, based on last year) could make 58 (or more) treys in 115 attempts. The answer is .008, a little less than 1-in-100, so what the Red Raiders are doing is already very rare statistically. Eventually, we may have to reject our "null hypothesis" that Texas Tech really has an underlying .390 probability on making threes.

As noted above, however, the larger the sample, the less susceptibility to unusually high or low success rates. To approximate a full season's worth of shots (i.e., a larger sample) instead of just a quarter season, I multiplied by four, Texas Tech's current number of made threes (58 X 4 = 232) and number of attempts (115 X 4 = 460). The ratio of 232/460 is the same as the Raiders' current three-point percentage of 50.4, but would be a much longer-term accomplishment. Again, using .390 as a baseline, the team's probability of hitting 50.4% of 460 three-point attempts is much tinier than before, .0000004, about 4 in 10 million.

Another potentially relevant concept that I'd like to mention briefly is regression toward the mean, which Lady Raider basketball announcer Ryan Hyatt sometimes invokes in his radio broadcasts. Regression toward the mean simply refers to the tendency for extreme values in the early rounds of performance -- either extremely high or extremely low -- to be followed by values more in the center of the distribution.

In conclusion, the statistical phenomena of small samples and regression toward the mean both suggest that the Texas Tech men will suffer some drop-off from their current 50.4% three-point shooting percentage. You probably don't need to have a statistics teacher tell you a 50% three-point shooting clip is unlikely to be maintained for a full season, any more than you need one to tell you that baseball players batting over .400 for the first month of the season will almost certainly fall off in their averages. If, however, you have some interest in the statistical concepts associated with teams' and players' fall-off after hot starts, you've visited the right place!

In about a half-hour, the Utah Jazz will attempt to improve upon its 12-1 start to the current NBA season (game-by-game log; ignore the pre-season games that are listed first). The Jazz finished exactly at .500 last year (41-41), so such a torrid start this season comes as a surprise to most observers. This article provides some ideas of why Utah appears to be so improved.

Happy Thanksgiving!

There was a men's college basketball game televised earlier today, in which Southern Illinois went scoreless in overtime in losing to Arkansas. Going scoreless in OT seems like an interesting type of cold hand.

Going scoreless for a five-minute stretch at any point in a game is probably fairly unusual. Further, if a game goes to overtime, that would seem to suggest the teams are pretty evenly matched (at least on that day or night). Therefore, one team shouldn't be able to shut out the opponent by sheer intimidation, for example by continually pressing and stealing the ball.

Shot clocks range from giving teams 24 seconds per possession to shoot in the NBA to 35 seconds in men's NCAA play (women's college ball uses 30 seconds, whereas the WNBA switched last season to 24 seconds from 30). Thus, unless both teams exhaust their full allotments of time to shoot, it would seem that teams could get about two possessions per minute, or 10 for an entire overtime. That's a lot of shots to miss (although a team could have fewer, due to turnovers), not to mention possible free throws.

One mechanism by which a team could go scoreless in OT -- of which you'll see some apparent evidence below -- is that it could get desperate after falling behind early in the extra period and then start jacking up threes.

I naturally wondered how often overtime shutouts have occurred. To get an estimate, I did some web searching using keywords such as overtime, scoreless, shut out and, to exclude other sports, basketball. It might not be the most scientific way to approach the problem, but it should provide a ballpark (or in this case, arena) figure. Below is a list of games I found from 2000 onward, complete with web links to game articles and box scores.

Men's College

Southern Illinois (vs. Arkansas), November 23, 2006
(SIU was 0-3 from the field in OT, no FT attempts)

George Mason (vs. James Madison), February 7, 2004
("The Patriots missed all six of their field goal tries, four from behind the arc, and went 0-for-2 at the free throw line in overtime.")

Women's College

Indiana (vs. Michigan State), February 29, 2004
(IU was 0-6 in OT field goal attempts, all from three-point land, no FT attempts)

Men's Pro

Boston (vs. Indiana), April 29, 2003
(first OT shutout in NBA play-off history; Celtics missed six shots from field and two FT attempts)

Vancouver (vs. Indiana), December 2, 2000

Women's Pro

None found.

With yesterday's 17-16 win over the Buffalo Bills, the Indianapolis Colts have gotten off to a 9-0 start this season. This makes them the only team in NFL history to start out 9-0 in two consecutive seasons. Last year, in fact, the Colts won their first 13 games of the season.

Obviously, winning regular-season games is not the problem for Indy - it's getting to the Super Bowl. We'll see if things are any better this season, come play-off time.

Some players in a given sport seem to perform at the same level night after night, whereas others show more variability from good to bad in how they do. Is it more advantageous to have one of type of player than the other? Sal Baxamusa investigates this question with regard to selected MLB starting pitchers, in The Hardball Times.

The Buffalo Sabres lost tonight to the Atlanta Thrashers, 5-4 in an overtime shoot-out. The loss, Buffalo's first of the season, means the Sabres must share the spot in the NHL record book with the 1993-94 Toronto Maple Leafs for best start to a season, at 10-0.

The 2006 World Series has just ended -- literally minutes ago -- with the St. Louis Cardinals closing out the Detroit Tigers in five games. Some notes from the perspective of streakiness:

Detroit pitcher Kenny Rogers, who was scheduled to go in a potential Game Six, will now have to wait for another year (and at age 41, he may not have many left in the game) to see if he can extend his current streak of 23 consecutive post-season scoreless innings. As shown in an ESPN graphic a few nights ago, these shut-out innings were compiled in three starts, one in each round of this year's play-offs: 7 and 2/3 against the Yankees, 7 and 1/3 against the A's, and 8 in the Tigers' lone win against the Cardinals. As shown in this article, the streak Rogers put together this post-season ranks among the best of all time. Should Detroit (or any other team Rogers pitches for) make the play-offs next season, all eyes will be on Rogers's throwing hand -- I mean, streak.

The Cards' David Eckstein, who got only two hits in his first 22 at-bats of this post-season, went 8-for-13 in the final three games against Detroit, en route to winning the World Series MVP award. For the Tigers, it was Sean Casey who had the hot bat.

Lastly, three stretches illustrate the apparent limitations of momentum. Both St. Louis and Detroit, of course, ended the regular season in slumps, yet made the World Series (see two articles in the links section on the right, addressing the issue of carryover from the end of the regular season to the play-offs). Also, the Tigers came into the World Series on a seven-game winning streak (three over the Yankees, four over the A's), yet took only one game from the Cards. It's not just that the Tigers lost the Fall Classic; numerous crucial fielding errors showed they were not at the top of their game against St. Louis.

Buffalo won again tonight in NHL action (3-0 over the New York Islanders), giving the Sabres a perfect 10-0 ledger. Buffalo's hot start ties the league record for most wins to begin the season.

Just one of those streaky days...

Michigan State took a 3-0 lead over Northwestern in their Big 10 football match-up, then fell behind 38-3 as the Wildcats scored 38 consecutive points. The Spartans then answered with 38 straight of their own, to win 41-38. In doing so, MSU set a new NCAA Division I-A record for size of deficit overcome to win (35 points).

If you look at the lists of the teams' drives (underneath the graphical diagram of scoring drives), you can see vividly what has to happen to produce a comeback like this -- one team gets amazingly hot and the other, similarly cold.

Prior to starting its comeback, Michigan State's last five possessions (excluding a brief one at the end of the first half) had consisted exclusively of punts and turnovers -- hardly a sign that the Spartans could put together four sustained touchdown drives (the other points came on a punt return TD and a field goal).

For Northwestern, the pattern was just the opposite. The Wildcats went from being able to move the ball up and down the field with apparent ease (at least that's what's implied by five touchdown drives) to their own stretch of entirely punts and turnovers -- including three straight "three and outs."

***

The Buffalo Sabres have opened up the National Hockey League season with a perfect 8-0 record, with tonight's win over the Boston Bruins. The Sabres are now two more wins away from tying the NHL record for most consecutive wins to start a season.

***

Finally, in tonight's World Series opener, won by St. Louis 7-2, Cardinal rookie Anthony Reyes retired 17 straight Tigers (i.e., nearly six straight innings of perfect baseball) after giving up a first-inning run. A graphic on the television broadcast noted that Reyes's streak was the best in World Series play since 1990, when Cincinnati's Jose Rijo put down 20 straight Oakland battersin the Reds' series-clinching Game 4 victory (see little game-by-game summaries on the right-hand side of the linked document).

I don't believe I've ever before drawn a hot-hand example from the Canadian Football League. Thanks to Phil Birnbaum's blog, however, there's always a first time.

Despite a nearly $200 million payroll and virtual all-star team for their starting line-up, the New York Yankees have once again stumbled in the play-offs, losing three games to one to the Detroit Tigers in the first round. The Yanks have not won the World Series since 2000.

I think many would agree that the team's breakdown occurred in two areas -- an aging and injury-prone starting pitching rotation and some shockingly poor hitting by a number of players who are typically very productive with the bat; the latter problem is discussed in this article.

The list below compares selected Yankees' 2006 regular-season batting averages (in parentheses) to their batting performances in the Detroit Series:

Robinson Cano (.342) 2-for-15

Gary Sheffield (.298) 1-for-12

Alex Rodriguez (.290) 1-for-14

Jason Giambi (.253) 1-for-8

Using an online binomial calculator, one can estimate the probability for each player of his getting as many hits (or fewer) as he did in the Detroit series purely by chance, given his (much higher) regular-season baseline batting average. Such probabilities are indeed low: Cano, .07; Sheffield, .09; Rodriguez, .06; and Giambi, .36. To reject a chance explanation, however, we typically require a probability of .05 or smaller (also known as "statistical significance").

For ARod, this latest poor performance in the postseason is nothing new. As the above-linked article notes, "Dating back to Game 4 of the 2004 American League Championship Series, Rodriguez has five hits in his last 46 postseason at-bats."

Here are some additional statistical observations from the baseball play-offs, by Elias Sports Bureau.

The St. Louis Cardinals' 8 1/2 game lead over the Houston Astros in the National League Central with only 12 games left (after the close of play on September 19) has almost completely evaporated. The Cards' lead now is only 1/2 game, with the final weekend of play remaining -- Houston at Atlanta, and St. Louis hosting Milwaukee (game-by-game logs for the Astros and Cards).

Presumably in connection with this dramatic turnaround, CNN/SI has posted its list of the greatest Pennant Race Collapses of all-time. To refer to these occurrences purely as "collapses" tells only half the story, in my view. In many (if not most) cases, one team's collapse was accompanied by another team's getting extremely hot. In some instances, the team making the comeback only won the pennant (league or divisional) by a single game at the end or in a special play-off after the seasonal standings ended in a tie. Thus, both the collapse by one team and the hot streak by the other were necessary for the latter to win out.

From CNN/SI's list, for example, the No. 2 entry involved the following from 1993: "On July 22, the Giants led Atlanta by 10 games. The Braves went 49-16 down the stretch to win the NL West by one game..."

And the No. 8 entry, the famous 1951 showdown between the Brooklyn Dodgers and New York Giants had this storyline: "On Aug. 11, the Dodgers led the Giants by 13 1/2 games, but the Giants won 16 in a row at one point and went 37-7 overall before winning a three-game playoff, which culminated in Bobby Thomson's Shot Heard 'Round the World."

In 2004, on the previous incarnation of the Hot Hand website, I did a fairly extensive analysis to mark the 35th anniversary of the 1969 NL East race, in which the New York Mets overtook the Chicago Cubs (this write-up is no longer posted here, but is available from me upon request). The following graph shows that, once again, both a hot streak by one team and a cold one by the other were implicated. The Mets ultimately won the division by eight games, so in this instance, they could have gotten by with a bit less torrid of a winning stretch.















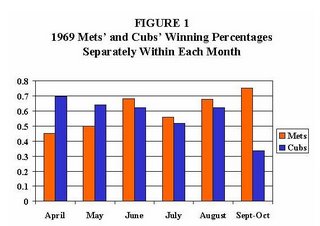
Will this year's Cardinals join the ignominious list of teams that squandered big leads and perhaps earn a special "honor" for doing it so late in the season? Stay tuned this weekend!

Byron Nelson, one of the all-time great golfers, died today at age 94. Among Nelson's many accomplishments was his record streak of winning 11 straight tournaments, which he did in 1945.

Tiger Woods is currently on his own streak, having won the last five tournaments he's played. In the above-linked article on Nelson's passing, Woods is quoted as follows:

"In this day and age, with this competition, to win 11 in a row would be almost unheard of," Woods said after his fifth straight victory when asked how Nelson's accomplishment compared with others, like Joe DiMaggio's 56-game hitting streak.

"What Byron accomplished, that goes down as one of the great years in the history of our sport. ... DiMaggio's record, I see that being broken more than winning 11 in a row."

In yesterday's pro football action, Washington quarterback Mark Brunell set a new NFL record with 22 straight pass completions. In looking over the play-by-play sheet (which can be accessed from the linked article), it appeared that many of Brunell's completions were short passes. Ultimately, however, a record is a record, and no one else had ever completed 22 in a row.

I didn't think the 2006 L.A. Dodgers could give us streakologists anything more to work with, beyond what they've already done this season! This is the team that, of course, lost 13 of its first 14 games after the All-Star Break, then immediately won 17 of 18, then later settled into a pattern one observer called "Consistent Inconsistency."

However, last night's Dodger miracle really takes the cake! Opening up the bottom of the ninth trailing 9-5 to San Diego, L.A. tied the game in a most unusual way -- solo homers by four straight batters. This particular feat had not been accomplished by any major-league team since 1964! (At the college level, though, we saw a team hit five consecutive homers earlier this year.)

Then, after the Padres took a 10-9 lead in the top of the tenth, the Dodgers won on a two-run homer by Nomar Garciaparra (ESPN.com article, play-by-play sheet).

Magnifying the significance of L.A.'s ninth-inning homer barrage further still, beyond the pressure of it being the ninth inning, the Dodgers and Padres are battling to the wire in the final weeks of the season for the National League West title (San Diego had entered the game 1/2 game up on the Dodgers, but Monday night's win now gives L.A. a 1/2 game lead).

The Dodgers most certainly don't have a Murderers' Row. In fact, they currently rank 15th in home runs out of the 16 National League teams.

To estimate the probability of the Dodgers' home-run burst, I first looked at the four batters who went yard (with their season-long home-run count and total number of official at-bats, which I found earlier today, in parentheses). In the order they batted, they are:

Jeff Kent (14 HR in 371 AB, ratio = .04)

J.D. Drew (17 HR in 460 AB, ratio = .04)

Russell Martin (10 HR in 378 AB, ratio = .03)

Marlon Anderson (9 HR in 244 AB, ratio = .04)

The probability of these four Dodgers putting together a string of four consecutive homers is thus:

.04 X .04 X .03 X .04 = .000002, or 1 in 500,000.

This calculation assumes independence of at-bats, like coin flips. One might argue that, if the same pitcher faced all four batters, he may have engaged in "streak pitching" to the same easy-to-hit part of the strike zone. An independence assumption may not be fully defensible, but it should be noted that the Padres changed pitchers after the first two homers, with relief ace Trevor Hoffman coming in (to no avail). The participation of multiple pitchers, along with multiple hitters, would seem to increase the independence of the events.

Can the Dodgers possibly top this?

Long Stretches of Alternating Wins and Losses

Some of you may recall a series of analyses I conducted back in January and February on the St. Louis University men's basketball team's remarkable pattern of alternating wins and losses for its first 19 games of the 2005-06 season (game-by-game log). In other words, the team won every odd-numbered game and lost every even-numbered game until it was 10-9 after 19 games. St. Louis then won its 20th game, which gave the team two straight wins, the first time two of its games had the same outcome.

Mathematically, I framed the problem as an "n choose k" question: If you had 19 little boxes lined up (one for each game) and 10 slips of paper with a "W" written on each (one for each win), where each box could hold either zero or one slip, in how many ways could you distribute the 10 slips into the 19 boxes? The answer, as obtained at this online "n choose k" calculator, was 92,378 different ways. This blurb mentions my analysis after SLU's first 17 games, at which point the team's alternation of a win, then a loss, then a win, etc., had roughly a 1-in-24,000 probability.

Frank Vaccaro has now looked into similar stretches in Major League Baseball history and he's also come up with a name for the phenomenon: Consistent Inconsistency. In an e-mail distributed to members of the Society for American Baseball Research's (SABR) listserve discussion forum, Vaccaro posted the following information (accurate as of the close of play on Friday, September 15, 2006):

You might notice that the Los Angeles Dodgers have been alternating wins and losses for the previous ten games. A loss tonight (very likely) will run their streak to eleven. [This indeed happened, then the Dodgers lost again, to end the alternation, as seen in their game-by-game log.] As I'm always on the lookout for regular-season predictors of post-season success, this caught my eye.

Consistent Inconsistency is not something that great, or even good teams, engage in... Other teams that engaged in long streaks of Consistent Inconsistency this year include Cincinnati, no surprise, 10 games, 6/19 to 6/29 and Atlanta, 10 games, 6/23 to 7/3. Toronto, already mentioned, would have also had a ten-game run of this stat had they lost yesterday -- but they won. This gave them two such streaks of nine games since mid-August.

Historically, there have been pennant winners who have had ten-game or more streaks of alternating wins and losses. Thirty-four teams, entering 2006, finished in first despite having alternating won-loss streaks of ten games or more, but this number jumps up as MLB adds divisions: 11 teams 1871-1968, 10 teams, 1969-1993, and 13 teams, 1994-2005...

Here are the number of occurences of these long streaks with only the most recent teams listed, entering 2006 (the date is the date of the start of the streak):

Streak--# of--
Length--Teams--Most recently accomplished by:

16--2--1981 LAn 6/7, 1974 PHIn 6/4.
15--3--1949 CHIn 8/16, 1913 CHIa 6/12, 1908 CHIa 4/28.
14--11--2005 COLn 9/17, 2001 MILn 8/22, 2000 CINn 6/20...
13--17--2000 FLAn 8/23, 2000 ANAa 8/18, 1992 OAKa 4/17...
12--29--2004 CHIa 8/24, 2003 HOUn 7/30, 2002 PITn 5/27...
11--77--2005 MILn 7/15, 2004 COLn 4/25, 2004 LAn 4/20...
10--118--2005 SEAa 8/28, 2005 LAn 5/2, 2004 PHIn 5/22...

257 STREAKS OF AT LEAST 10 G ALTERNATING WINS AND LOSSES

This makes the Dodgers the 249th team on the list. Eleven teams had two such streaks during their season.

Jelena Jankovic, a tennis player I'd never heard of prior to today, has reached the semi-finals of the U.S. Open women's singles bracket. As with golf, there are so many men's and women's tennis players out there that it's not unusual for someone I've never heard of to do extremely well in a major tournament.

What makes Jankovic's case unusual -- and interesting to me as an observer of streaks -- is that, in the early months of 2006, she lost 10 straight matches. Given tennis's single-elimination format, she thus went from city to city, getting eliminated each time after one match.

However Jankovic did it, she was able to turn things around, making the quarter-finals (final eight) or better in several later tournaments. I'll have to think about what kinds of analyses I could do. For now, though, her winning streak of five straight matches at the U.S. Open is something to behold.

My specialty on this blog is, of course, the statistical analysis of sports streakiness. It has not been my intention to exclude other, non-statistical perspectives on hotness and coldness; I just haven't seen much of other genres.

Now, however, I've just finished reading the book Confidence: How Winning Streaks & Losing Streaks Begin & End (excerpt), by Harvard Business School professor Rosabeth Moss Kanter. The original hardcover version came out in 2004, but the paperback, which I read, just came out this year. Focusing on the worlds of business and sports, the book examines long-term failures, successes, and turnarounds from one to the other, through the lens of organizational culture.

In the athletic realm, Kanter uses two women's collegiate teams, North Carolina soccer and UConn basketball, to present the most extensive case studies of winning cultures, the Prairie View A&M football squad to illustrate a losing culture, and the Philadelphia Eagles' ascension to Super Bowl-quality in recent years to demonstrate positive turnaround. Dusty Baker's Chicago Cubs, who at the time of the book's initial publication looked to be turning around the franchise's longstanding losing ways (although they're not doing so at present), are discussed more briefly, as are several other teams.

What I take to be Kanter's major points are as follows:

*An organization's most visible results -- on the scoreboard or in financial data -- will tend to be reflected at a deeper level by other markers, such as a leader's communicative skills and ability to innovate (and spur innovation) and a team's work ethic, quality of facilities, community support, etc.

*Winning -- or losing -- can launch "chain reactions," thus perpetuating the original trend. Winning gets a team on television, helps attract better players (either through free agency in the pros or recruiting at the college level), builds fan support, etc., which fosters further winning, brings in money to improve facilities, etc. Losing sets the opposite types of events in motion.

*The ideal psychological environment for an organization seems to be one in which employees know they'll be held accountable for maintaining productive output, but feel supported enough that they will be comfortable taking risks, innovating, and reaching out to colleagues in a collaborative spirit. Failure of a promising idea to bear fruit will not trigger a cycle of criticism and blame, but rather a coming together of employees to improve the next time.

These ideas certainly seem valid. The tricky part -- which Kanter readily acknowledges -- is in untangling the causality. Yes, a positive attitude (or nice facilities or fan support) can help a team win, but winning will also likely promote a positive attitude (and the ability to construct new facilities and to attract fans).

Implementing Kanter's suggestions could well spur a winning streak, but even if a team doesn't end up winning as much as it had hoped, the changes could still be a net positive. One example I've thought of is that a university that attempts to improve its national academic ranking by building a new libary, will still have a nice new library, regardless of what happens with the rankings. Ultimately, however, there are no guarantees. I suspect there are many sports teams Kanter did not talk about that work hard in practice, assess player performance via objective "metrics," have nice facilities -- and still lose.

Statistical hot-hand research, that is, whether outcomes of successive trials on sports tasks are independent or not, is discussed occasionally in the book -- including citation of the Gilovich et al. study and a reference to Duke men's basketball coach Mike Krzyzewski's philosophy that players should always focus on the "next play," without carrying over any reaction from the previous one (p. 351). Most of the book's subject matter deals with long-term trends, however, and not moment-to-moment performance.

At 380 pages, the book will require dedication from the reader. Many portions seemed redundant to me, and full of platitudes. Often, the text jumps from one team/organization to another. My favorite parts were the extended discussions of single case studies, such as Prairie View football, Continental Airlines, and Nelson Mandela's leadership in transforming South African society.

I wanted to tie a bow to wrap up three stories I had written about earlier this month:

With their 7-2 win over Boston this afternoon (and the day off tomorrow), the Oakland A's have completed their August games with a 21-6 record (game-by-game log). As I discussed originally in my August 8 posting, the A's have shown an amazing tendency to get hot in August, going back several years. From 2001-2006 inclusive, Oakland's record for games in August is 124-45 (.734)...

A couple of Sundays ago (August 20), I wrote about the Seattle Mariners' record 20-game losing streak within their own division, the American League West. In the time since, the M's have really turned things around (log). After August 20, Seattle went outside of the AL West, winning five out of six games (combined) against the AL East's New York Yankees and Boston Red Sox. These wins, of course, did nothing to end the Mariners' AL West losing streak, but seemed to suggest Seattle had righted the ship. The Mariners then returned to AL West play a couple nights ago, shutting out the Angels 2-0. And tonight, the M's go for a three-game sweep over the Halos...

The Houston Astros' Willy Taveras, about whom I wrote in the posting immediately below the current one, had his consecutive games hitting steak end at 30 on Tuesday night.

The Houston Astros' Willy Taveras has just extended his hitting streak to 30 games, beating out a dribbler toward third base in the first inning at Pittsburgh (I get most Astro and Texas Ranger games on cable TV in Lubbock, Texas, where I live).

The 30-game mark is when I'll generally start to write about hitting streaks. Thirty is a nice round number, and is a little over halfway to Joe DiMaggio's record of 56 games with at least one hit per contest.

It'll probably be several more games before I start presenting calculations of Taveras's probability of catching DiMaggio. To get a feel for the nature of these calculations, however, you can look at this write-up I did for the Phillies' Chase Utley, back when he had a nice streak going (which reached 35 games before ending).

The Seattle Mariners have closed out the weekend losing their 20th straight American League Western Division game, 3-2 to the Angels. In terms of consecutive losses within a team's own division, the Mariners have comfortably surpassed two other teams (the 2004 Diamondbacks and 1993 Rockies) who each lost 16 straight divisional games. It was not until 1969 that Major League Baseball -- having expanded from 20 to 24 teams -- introduced Eastern and Western divisions within each league. Prior to that, all the American League teams competed in one set of standings, as did all the National League teams, with the two first-place finishers going directly to the World Series.

The L.A. Dodgers' amazing turnaround continues. The Dodgers started off the second half of the season, right after the All-Star Break, by losing 13 out of 14. They've now rebounded by winning 17 of 18 (second half game-by-game log).

Jon Weisman at Dodger Thoughts conveys the strangeness of it all in this essay, a brief excerpt of which follows:

Why does the best Dodger 18-game run in 107 years and best National League run in 20 years feel so unreal? ... A .533 team playing .944 ball after an .071 stretch is hard to wrap the brain around.

(I interpret "best National League run" to mean by any NL team, not the Dodgers' best run through the NL.)

On the SABR members' e-mail discussion forum, the Dodgers' recent streakiness prompted an inquiry into other abrupt turnarounds (thanks primarily to Bob Timmerman and Frank Vaccaro for their messages). Examining the longest win-only stretches followed immediately by the longest lose-only stretches (or vice-versa), the most common patterns involved stretches of around 8 or 9 games won (or lost) and then 8 or 9 lost (or won). The greatest total number of games listed, in which a team's sequence consisted only of a fairly long winning and losing streak, was 21: The 1927 Detroit Tigers won 13 straight, then lost the next 8, from August 10-31 of that year (log).

A dramatic example I recalled is that of the 1987 Milwaukee Brewers. The Brewers started off the season with 13 straight wins. The losing streak did not come immediately thereafter, but it wasn't long before they lost 12 straight (log).

There were a couple of instances of hotness and streakiness in today's 13-0 Cleveland win over Kansas City.

Travis Hafner hit his sixth grand-slam homer of the season, tying Don Mattingly's MLB record. As the linked article notes, "Hafner is 8-for-13 with six homers and 29 RBI this season with the bases loaded." What this means is that, on nearly "Haf" of his bases-loaded at-bats, he has homered (6 of 13)!

The thing about a bases-loaded situation is that, in order to avoid walking in a run, the pitcher is under pressure to keep the ball around the strike zone. This, in turn, presumably allows the batter to concentrate on a smaller area in following an incoming pitch. I'm certainly not saying this accounts completely for Hafner's grand-slam rate, but it's probably a factor.

Hafner's offensive punch was not isolated, however. Cleveland took an 11-0 lead in the first inning, with "[t]he first 10 Indians to bat all reach[ing] base and scor[ing] against Luke Hudson (5-4)."

If it's August, it must be the Oakland A's getting hot again. As of this writing (mid-day Tuesday), the Athletics are 5-1 for August, plus they were also 5-1 in their last six games of July, for a 10-2 stretch overall (game-by-game log for second half of this season).

Looking at the records for previous A's seasons in Baseball Reference, here's how they've done each year of this decade in August:

2000 -- 11-16 (but 21-7 in September)

2001 -- 22-7 (along with 19-8 in July, 17-4 in September, and 6-0 in October)

2002 -- 24-4 (their 20-game win streak was mostly in August, but carried over into September, for which they were 18-8)

2003 -- 20-9

2004 -- 20-8

2005 -- 17-11 (although not as strong as June's 19-8 and July's 20-6)

Excluding 2000, Oakland is 108-40 (.730) in August since 2001.

I haven't decided yet what statistical analyses I might do of this trend. I, like many other people, did analyses to estimate the probability of the A's 2002 winning streak.

I'm pleased to note that in the July 2006 issue of Computers and Operations Research, Donald Martin has just published an article entitled "Hot-hand effects in sports and a recursive method of computing probabilities for streaks,"in which he cites and extends my analysis of the 2002 A's.

The Angels and Rangers are playing an afternoon game today, which will be starting shortly. As I've been documenting the last couple of days, the Halos' Vladimir Guerrero has gotten at least one hit in every game he's ever played against the Rangers, 44 games in all. Can the Texas pitchers finally hold him hitless in a game? We'll soon see. Below, I provide real-time commentary...

The Rangers intentionally walk Guerrero in the first inning, with two outs and a runner on second. I think that's a strategically defensible move. The FOX television crew puts up a graphic indicating that Guerrero has a .443 lifetime batting average against the Rangers! (The .443 figure is also documented here, in the Preview section below the box score.)

[As an aside, I'm curious whether all of Guerrero's games against Texas have been as a member of the Angels, for whom he has played since the start of the 2004 season. Vlad, of course, played many years for the National League's Montreal Expos (now Washington Nationals) before coming over to the AL. But, with interleague play, the Expos could have faced the Rangers.

I initially consulted Baseball Reference, finding the Rangers' game-by-game log for 2003. Sure enough, the Rangers played the Expos in a three-game series from June 6-8, 2003. I then looked up the box scores of these games on Retrosheet, and noticed Guerrero was absent from all three. Further research confirmed my guess that he had been injured, this MLB document showing a June 9 action in which Guerrero was placed on the DL, retroactive to June 5. There do not appear to have been any prior interleague Texas-Montreal games.]

Guerrero walks again in the third, the Rangers' John Koronka clearly seeming to be pitching around him. Vlad is known as a free-swinger at the plate, but some of the pitches he was just thrown were too far out of the strike zone even for him.

Another intentional walk in the fourth, in the same situation as earlier: man on second, two outs.

Yet another intentional pass in the sixth inning, with a runner on third and one out.

An amazing catch in right field by the Rangers' Mark DeRosa on a tricky fly ball thwarts Guerrero in the bottom of the eighth. DeRosa was running toward the wall in a somewhat circular path to keep track of the ball and may have been bobbling it as he fell to the ground, but there wasn't any argument over the "out" call. Baseball, of course, has no replay rule, and anyway, none of the camera views provided a conclusive view of what happened. If you look at the linked biographical page on DeRosa, he's listed as a second baseman, but he certainly showed a lot of dexterity in the outfield on Guerrero's fly ball.

That will almost certainly end the streak, as the Angels are unlikely to need their ninth-inning at-bats, leading 10-3.

Yep, the Rangers go down quickly in the ninth. Streak over.

Update: A video of DeRosa catching Guerrero's fly ball is available here. When the new page comes up, select "Top Play: 350 K." First, you will see a different play from the game. When that play is over, look over to the lower-right portion of the page, where some plays are listed (the first one being "Rivera's three-run homer"). Then, scroll down to "DeRosa's falling catch," and select it.

Utley-Guerrero Watch

Chase Utley has struck out in the first inning of the Phillies' game against the Mets.

Utley is retired in the third inning on a fly ball to center.

A fly-out to center again in the fifth for Utley.

The streak's going down to the wire -- Utley grounds out in the seventh.

Utley will be the Phillies' lead-off hitter in the top of the ninth. This will probably be his last at-bat, unless the game goes extra innings. Philadelphia currently leads 4-3 over the Mets.

Utley strikes out in the ninth.

Phillies-Mets game over. Utley streak over at 35 games.

Meanwhile, on the opposite coast, the Angels' Vladimir Guerrero has struck out in the second inning against Texas.

Guerrero singles in the third, so he now has at least one hit in all 44 games he's ever played against the Rangers.

According to this article, which I've added after the game, Guerrero "went 2-for-4 to extend one of baseball's most peculiar streaks. He has hit safely in all 44 games he has played against Texas in his career, the longest stretch by any player against one team since 1957 -- which is as far as Stats Inc. has been able to research it."

For background on these hitting streaks, see my Thursday, August 3, posting.

7:10 pm Central: Baseball fans will be keeping their eyes on two ongoing hitting streaks tonight, one front and center on the MLB landscape and the other more under the radar.

The prominent streak is that of the Phillies' Chase Utley, who last night extended his consecutive hitting stretch to 34 games. In fact, even before I can finish this write-up, Utley has singled in the first inning at St. Louis, extending the streak to 35 games [game article, added later].

He now is 21 games away from tying Joe DiMaggio's legendary 56-game hitting streak. I will analyze Utley's chances of reaching 56 games, later on tonight.

A little over 90 minutes from now, the Angels' Vladimir Guerrero will try to preserve the "other" streak I alluded to. Guerrero has gotten at least one hit in every game he has ever played against the Texas Rangers, 42 games in all.

This article from May, when the Angels and Rangers last met, documents the magnitude of Vlad's accomplishment: the next-longest actively going hitting streak by a player against the same opponent was 18 games (as of when the article was published), and the next-longest hitting streak of this type held at any time in the past by a currently active player is 35 games.

8:30 pm Central: With the Rangers at Angels game about a half-hour away, I thought I'd provide an estimate of Chase Utley's probability of equalling Joe DiMaggio's record 56-game hitting streak.

First, we need a prior (baseline) batting average for Utley. A good figure to use is .290. After his last game of the present season (to this point) without a hit, on June 21, he was batting .290. Also, his batting average for 2005 was .291 (year-by-year stats), so prior to the current hitting streak, Utley appeared to have a stable, long-term average of around .290.

The .290 represents Utley's probability of getting a hit on any single at-bat. However, because a player will usually get around four at-bats per game, the probability of getting at least one hit in a game is considerably higher than the batting average.

Fortunately, a chart exists that allows easy conversion of a batting average into the probability of at least one hit in a game. In Table 1 of the linked document, the closest shown batting average to .290 is .300, which translates into a probability of .745 of getting at least one hit in a game.

We then simply raise .745 to the 21st power (given that Utley's 21 games away from tying DiMaggio), which yields .002, or 1-in-500. This calculation assumes independence of observations, i.e., performance in one game does not affect performance in the next.

Also, as noted in the first linked article in tonight's entry (back up under the 7:10 pm heading), Utley is batting .401 during the streak. A .400 average converts to a .855 probability of gettting at least one hit in a game; .855 to the 21st power is .04, or 1-in-25. This latter estimate, though optimistic, still shows a small likelihood.

10:35 pm Central: A little while ago, Vlad Guerrero homered in the bottom of the fourth inning. He thus has gotten at least one hit in all 43 games he's ever played against the Rangers [game article, added later, which characterizes Guerrero's feat as "the longest such streak against an opponent in the majors for at least 50 years"].

Right here in Lubbock, at Texas Tech University's Rawls golf course, located about a mile and a half from my office, a 53-year-old gentleman named Danny Leake shot a hole-in-one at the same hole (the sixth) this past Saturday and Sunday. According to the article in the Lubbock Avalanche Journal (registration required), the hole had distances of 174 and 178 yards the two days, differing as a result of pin placement on the green.

I was very pleased to see the A-J article probe the statistical aspects of Mr. Leake's accomplishment, drawing from a set of probability estimates of various hole-in-one phenomena made years earlier by mathematician Francis Scheid for Golf Digest. Scheid's estimates are also shown here, in the yellow-shaded sidebar to a 2005 Golf Digest article (toward the bottom of the page that comes up).

What Leake exhibited is nothing, if not a hot hand, so I had to pursue the topic further. The neatest thing I found was an amazing USA Today page on holes-in-one, which includes links to a compilation of all aces on the PGA tour from 1990 to mid-2006, and to a similar compilation for the LPGA tour (beginning in 1992).

The sidebar accompanying the aforementioned 2005 Golf Digest article stated, among other things, that the odds of an "[a]verage player acing [a] 150-yard hole" were 80,000 to 1, and for a 200-yard hole, 150,000 to 1. Technically, odds are not the same thing as probabilities, but for extremely rare occurrences, the terms converge.

As noted above, the hole that Leake aced twice had a distance of roughly 175 yards from the tee, halfway between the two figures cited in the previous paragraph. Let's use the odds for a 150-yard hole (80,000 to 1). At this point, I'd like to introduce a new twist; some may disagree with this way of addressing the question, but it seems reasonable to me. Even though there are 18 holes in a round of golf, holes-in-one seem to come exclusively (or almost exclusively) on par-3 holes. Texas Tech's Rawls course had four such holes, numbers 3, 6, 10, and 16. In two days, a golfer would thus get to play par-3 holes eight times total.

We can then ask, given a prior probability of 1-in-80,000 (.0000125) of a hole-in-one from a single attempt off the tee, what is the probability of someone acing two (or more) holes in eight opportunities? An online binomial calculator tells us that such probability is .000000004 or 1-in-250 million.

That, however, would be for making a hole-in-one on any two holes out of eight (i.e., the two aces could come from among the four par-3 holes on one day, or from one hole each on the two days and, if the latter, they could be on same hole or different holes).

We have to restrict the situation to scoring the aces on the same hole both days. I've created a chart (below) to illustrate that there are 28 possible ways to ace two holes out of eight, some on the same day, others on different days. The main diagonal is removed (signified by black X's) because, for example, a golfer could not ace Hole No. 3 twice the same day. The 28 blue X's above the diagonal indicate redundancy with the 28 cells below the diagonal. The cells with no X's thus represent the 28 possible ways to ace two holes out of eight. Finally, there are only four cells (indicated by red asterisks) where the golfer would be acing the same hole on back-to-back days. So, among the 28 ways to get two holes-in-one out of eight holes generally, only four ways fit with what happened in Lubbock, and of course 4/28 = 1/7.



We thus multiply our prior value of 1-in-250 million by 1/7, yielding 1 in 1.75 billion. That's my best guess!

Just a few quick items in connection with today's Major League Baseball action...

When I saw the Houston Astros were pinch-hitting for Brad Ausmus late in this afternoon's game against Arizona, it reminded me of a write-up I was planning to do.

A little while back, a discussant known as "TechTown" on the RaiderPower.com Texas Tech sports chat site pointed out that Ausmus had gone through a 0-for-40 hitting drought in late June and early July. Hence, it was no surprise to me when Ausmus was lifted today.

Looking at Ausmus's statistics, for the last couple of years and for his career, he's roughly a .250 hitter. That means that on any given official at-bat, he has about a .75 probability of making an out. Raising .75 to the 40th power (for the length of the slump) yields .00001 as the probability of Ausmus's drought, assuming independence of at-bats (i.e., that the outcome of any one at-bat has no effect on the next at-bat, like coin-flipping).

In other news, the Cubs recorded their first home four-game sweep of the Cardinals since 1972, and the Mets swept the Braves in Atlanta for the first time since 1985.

I typically don't write much about tennis. However, I've just been watching taped coverage on cable television's Tennis Channel of the Dominik Hrbaty-Robby Ginepri quarter-final match in the Countrywide Classic from UCLA's L.A. Tennis Center (UCLA being my undergraduate college alma mater).

I came across the match midway through, and when I heard the announcers saying that Hrbaty had won several straight points, my ears naturally perked up. Being the streak fanatic that I am, I kept rooting for Hrbaty to win more points (or conversely for Ginepri to lose more points) and it kept happening. By the time Hrbaty's run ended, he had won 18 straight points!

This summary on the men's ATP tour website says that Hrbaty won 19 straight points. But even by its own enumeration of the sequence, the article confirms it was actually 18 points:

After a tight start to the match Domink Hrbaty blew open his quarterfinal with Robby Ginepri, winning 19 straight points at one stage en route to a 7-6(0), 6-2 win.

Hrbaty won 19 straight points starting with the last point of the 12th game of the opening set. He then won the tie-break to love, held serve to love to open the second set, then broke Ginepri to love in the second game. He won the first two points of the third game before conceding the first point to Ginepri with a double fault. Ginepri won just 19 second set points.

Last point of the 12th game of 1st set = 1
Tie-breaker 7-0 = 7 (8 cumulatively)
2nd set, 1st game at love = 4 (12 cumulatively)
...........2nd game at love = 4 (16 cumulatively)
...........3rd game, first 2 points = 2 (18 cumulatively)

Inquiry into streakiness -- and other statistical phenomena -- in tennis is not limited to anecdotes, however.

Economist Franc Klaassen of the Universiteit van Amsterdam, in collaboration with Jan Magnus, has published a number of articles on tennis (click here for a list of Klaasen's publications, containing links to the articles themselves). Of particular interest to aficionados of streakiness is the following article:

Klaassen, F.J.G.M. and J.R. Magnus (2001), “Are Points in Tennis Independent and Identically Distributed? Evidence from a Dynamic Binary Panel Data Model,” Journal of the American Statistical Association, 96, 500-509.

By "independent," researchers mean that the outcome of one point has no bearing on the outcome of the next, just like coin-flipping. The opposite would be "dependence," as in streakiness or momentum, where winning one point would increase one's probability of winning the next point.

The aforementioned article studied singles play at Wimbledon. Putting aside the intense statistical aspects, Klaasen and Magnus reached the following conclusion:

The independence hypothesis... is rejected with a p-value of 1.7% (men) and 0.3%(women)... Winning the previous point has a positive effect on winning the current point, both for men and for women,...

(Readers with statistical training will know that for a result to attain "statistical significance," it must have a probability of 5% or less [p < .05] of occurring purely by chance.)

Tennis, in fact, is one of the few sports in which streakiness (or momentum) appears to be fairly well documented, in not just the Klaasen and Magnus study, but also in earlier research by Jackson and Mosurski. Studies of tasks such as basketball shooting and baseball hitting generally have not been able to reject independence (in the various links sections on the right-hand side of this page, see the pages of S.C. Albright, Tom Gilovich, and Jay Koehler, as well as the link to a hot hand bibliography further down, for details).

About two months ago, while attending a conference on networks at Indiana University Bloomington (see photos on another of my blogs), I visited with psychology professor Steven "Jim" Sherman, whom I have known for over 20 years. I first met Jim in the spring of 1984, while visiting IUB on a trip to look at potential places to go to graduate school (I ultimately chose the University of Michigan).

I would occasionally see Jim at conferences over the years, and then out of the blue, I got a call from him some time in the fall of 2002. Jim invited me to a small, informal conference he was co-organizing on statistics and sports decision-making to be held in March 2003 in Scottsdale, Arizona (to enable conference attendees to attend spring training if they wanted!). A photo of the participants in that gathering is shown below.



Jim is shown front and center in the shorts, flanked to his right by University of Chicago professor Richard Thaler, the other co-organizer. Right behind Jim is Cornell's Tom Gilovich, who was the lead author on the 1985 article that introduced hot hand research. Right behind Tom (skipping the gap in the third row), is me, at the center of the back row. To my right is legendary baseball analyst Bill James, and in front of Bill, to his right, is fellow baseball expert Rob Neyer.

Anyway, back to my visit with Jim in May 2006. As I was entering his office for our meeting, I noticed he had a letter Scotch-taped to his door. The letter, dating back more than 20 years, was from former Indiana men's basketball coach Bob Knight, now, of course, the coach where I'm located, Texas Tech University. And the letter pertained to, of all things, the hot hand. As it turns out, Jim had sent Coach Knight a copy of the aforementioned mid-1980s article by Gilovich and colleagues, and Knight had sent this reply...



The letter has been on Sherman's door for over 20 years, for all passersby to see. Given the letter's status as an historic artifact (sometimes spelled artefact) in the annals of hot hand research, I asked Jim if we could make a copy of it for posting on my website, and he agreed. (I figured that most people probably wouldn't want their signature broadcast to the world, so I blocked out Coach Knight's.)

Coach Knight's skepticism of hot hand research -- the general finding of which is that making one or more shots in a row does not tend to raise a shooter's likelihood of making the next shot -- has been reported previously, in this Wikipedia entry on the "Clustering Illusion" (of which I am not the author). Still, I thought it would be neat to display a copy of the original letter. By the way, Boston Celtic coaching great Red Auerbach has also expressed skepticism.

Knight is absolutely right about the multitude of factors that determine whether a basketball shot will go in or not. Many researchers have voiced similar concerns, such as the possibility that the inability to detect streakiness could stem from players who just made a shot being guarded more closely the next time, or feeling more confident and shooting from farther away. In an attempt to eliminate as many extraneous factors as possible, researchers have used controlled shooting exercises, such as the NBA three-point shooting contest the night before the All-Star Game. Still, little evidence of streakiness has been observed (see the Koehler & Conley [2003] paper at the following site).

Chipper Jones of the Atlanta Braves saw his streak of 14 straight games with an extra-base hit end tonight. He had tied the previous major-league record.

I recently returned from Seattle, where I attended the Society for American Baseball Research (SABR) conference and presented a research poster entitled "Top Major League Baseball Streaks of 2005."

To the right is the city's famous Space Needle, of which I snapped a picture. The Space Needle is part of the larger Seattle Center complex.

Below, I'm standing in front of my poster, clad in a mid-late 1970s, Bill Veeck-inspired Chicago White Sox jersey. Baseball garb is a common form of attire at SABR meetings.



In my poster, I displayed brief synopses of several occurrrences from 2005 that stood out to me, either in terms of estimated statistical rarity or historical significance (i.e., time since previous similar occurrence). Here are the streaks...

Philadelphia’s Jimmy Rollins ended the 2005 season on a 36-game hitting streak, tying him (at the time) for 10th on the all-time list. According to the July 14-19, 2005 USA Today Sports Weekly (providing statistics through roughly the first half of the season), Rollins was batting .273, which converts to a baseline probability of roughly .710 of his getting at least one hit in a game (because a player usually gets multiple at bats in a game, the probability of his getting at least one hit is generally pretty high). This latter probability is raised to the 36th power (length of the streak), yielding as the probability of the streak, .710^36 = .000004.

In August 2005, the Florida Marlins went 25 straight games with no one other than Miguel Cabrera or Carlos Delgado homering (game-by-game log for second half of 2005 season). Using June and July games as a baseline (where at least one Marlin other than the “big two” had homered in 19 of 53 games, .358, or a failure rate of .642), the probability of the drought was .642^25 = .00002.

Poor performance from the Kansas City Royals is not unexpected. Still, when a team loses 19 straight games (as the Royals did in 2005 from late July well into August), it’s noteworthy (game-by-game log). Before the streak, KC had a 38-63 record, for a winning percentage of .376; conversely, this is a .624 losing percentage, which when raised to the 19th power = .0001. (Steve Levitt also looked at the Royals' losing streak last year.)

Seattle’s Ichiro Suzuki, who in 2004 set the single-season record for most hits, suffered through a 0-for-22 slump (longest of his career) in early August 2005. The mid-season Sports Weekly listed him as batting .311 (a failure rate of .689), so the probability of Ichiro’s going hitless in 22 straight official at-bats is .689^22 = .0003.

From mid-July 2005 on, the Red Sox won 19 of 20 at home (log). Boston’s home winning percentage prior to this stretch was .581. Using a binomial-statistic calculator, the team’s probability of winning 19 (or more) out of 20 was roughly .001. (This calculation probably overstates rarity of this hot stretch, as opponents included Tampa Bay, Minnesota, Kansas City, and Texas, plus Chicago White Sox.)

Finally, the 2005 White Sox recorded many impressive streaks:

They won 16 of their last 17 games (5 regular season, 11-1 in post-season). Based on their .611 winning percentage through the end of August, the probability of their winning 16 (or more) games out of 17 was approximately .005. (Cleveland made a late-season run rivaling that of the 1969 New York Mets, but it wasn’t enough to catch the Sox.)

Chicago pitchers recorded four straight ALCS complete games vs. the Angels, a similar post-season achievement not having occurred since Yankee pitchers threw five straight complete games in the 1956 World Series.

Chicago pitchers again worked their magic, not allowing the Astros a hit in their final 29 World Series at bats with runners on base, unprecedented in World Series play since the 1966 Dodgers (31 at bats).

I also mentioned some streaky developments from thus far in 2006 on my poster. Two of them I've already blogged about here (shown below), the University of South Carolina's five straight homers in NCAA play-off action against Georgia (June 12, 2006 entry) and Vladimir Guerrero's hitting against the Texas Rangers (June 5, 2006 entry).

Two additional 2006 streaks I noted on my SABR poster were the Yankees' streak of 10+ hit games and Boston catcher Jason Varitek's homering every May 20 for five straight years (2001-2005), a run that ended in 2006 (thanks to Indiana University professor Jim Sherman for bringing the latter streak to my attention).

Below are some additional photos I took of the SABR poster session (here's the official list of posters, including summaries).

This year's NBA championship series is now over, with the Miami Heat defeating the Dallas Mavericks 4 games to 2. There were several instances of streakiness in the series, not least Miami's coming back from 2-0 down (and in great danger in Game 3) to take four straight. Each of the teams, as well as individual players, also went through periods of hotness and coldness, of course. Once the Heat began to turn the series around, Dwyane Wade went through stretches where it looked like he couldn't miss (and rarely did). At the other end of the spectrum, the Mavs' outside shooting during the second half of Game 6 seemed to disappear.

What I'd like to focus on here, though, is the dreadful free throw shooting of Miami center Shaquille O'Neal, whose statistics are available here. As all NBA fans know, even under the best of circumstances, Shaq is terrible from the stripe, making only 52.8% of free throws for his career (based on nearly 10,000 attempts!).

This past regular season, O'Neal slipped to 46.9% on free throws, then to 37.4% for the play-offs (68 of 182). In the finals against Dallas, Shaq's FT shooting was particularly hideous, 29.2% (14 of 48). In three of the games against the Mavs, he shot 1 of 9, 1 of 7, and 2 of 12.

Before possibly examining the depths of O'Neal's woes vs. Dallas, I think it's worth testing initially whether the roughly 10% drop in his FT percentage from the regular season to the play-offs overall is statistically significant. With a dichotomous outcome such as hit or miss on a free throw, a statistical technique known as the binomial probability (for which there's an online calculator in my links section, to the right) is very useful. It answers the question of how likely a given pattern is (i.e., a certain number of hits within some number of attempts), given some prior baseline percentage of success.

In Shaq's case, how likely is it that he would have made 68 (or fewer) free throws out of 182, assuming a baserate of .469 (corresponding to his FT percentage in the regular season)? Using the aformentioned calculator, this probability is .006, sufficiently small to be considered statistically significant (cut-offs of .05 or .01 are commonly used).

Thus, even when we take Shaq's play-off FT performance as a whole (not focusing merely on his horrible time in the final round), his fall-off from the regular season is more than would have been expected from ordinary fluctuation. Fatigue is a possibility, especially since his worst round in the play-offs was the last one. However, Shaq and the Heat had a six-day rest from the end of the Detroit series (June 2) to the start of the Dallas series (June 8), and he still went 1 for 9 from the line in the opener against the Mavs.

If anyone would like to conduct statistical analyses of other players in the Miami-Dallas series, please do so. You can provide a brief write-up of what you found in the comments section below.

Leading up to this past weekend, I had been planning to write something about how the men's French Open tennis final would be pitting two players against each other, who each had phenomenal streaks coming in. That indeed happened and I will still write about it, but something else happened over the weekend in college baseball, which I think tops the tennis match.

The University of South Carolina hit a mind-boggling five consecutive home runs against the University of Georgia, en route to a 15-6 win and 1-0 lead in the teams' two-out-of-three super-regional series (final qualifying round before the College World Series).

A simple way to estimate the probability of five homers in five at bats is to start with the Gamecocks' baseline probability of hitting a home run in any single at bat. This Southeastern Conference (SEC) baseball statistics page (updated through June 6, as I'm looking at it) tells us that, out of 2,215 at bats this season, South Carolina had hit 82 homers (.037).

Alternatively, we could increase the denominator by adding in plate appearances that are not counted as official at bats. The main source of such extra appearance are walks, however, and one could argue that many walks represent instances where the pitcher does not want to give the hitter the opportunity to swing the bat (explicitly, when there's an intentional walk, but also when a team "pitches around" a hitter). Also, by using only official at bats as the denominator (and thus keeping the home run ratio a little higher), that will make my upcoming calculation a little more conservative (i.e., helping to avoid overstating the rarity of the occurrence).

We then simply raise the Gamecocks' probability of a home run on a single at bat (.037) to the fifth power (representing the five homers), which yields .00000007 (7 X 10 to the minus eighth power, or 7 in 100 million). This type of calculation is analogous to determining that the probability of rolling double sixes on two dice is 1/36, by raising the probability of a six on a single die (1/6) to the second power.

In the dice example, it is assumed that the outcomes of the roll of two dice are independent (i.e., the number that comes up on one die does not affect the number that comes up on the other). One may question whether the independence assumption holds up in this home run-hitting scenario. Many of you are probably thinking that the same Georgia pitcher was throwing to these batters and just kept "grooving" the ball to the hitters, based on loss of speed and/or movement on the pitches. That may be true to some extent, but it must be noted that after the first three homers of the streak, Georgia changed pitchers and the new guy gave up two more homers!

Another consideration is that I was drawn to analyze the South Carolina streak by its spectacular nature. If we were to ask instead, in all the countless college baseball games played over a period of years, how likely is it that we would find such a streak at some point, the streak would not seem so unlikely.

Here is a passage from the textbook I use in teaching statistics (King & Minium, 2003, Statistical Reasoning in Psychology and Education, p. 205):

Let us consider again the case of Evelyn Adams... who won the New Jersey Lottery twice in a 4-month time span in 1986. The probability of Ms. Adams doing this was 1 in 17 trillion... If there were 4,123,000 lottery tickets sold for each lottery, and Ms. Adams had purchased 1 ticket for each, the probability of her winning both was (1 / 4,123,000) (1 / 4,123,000), the same as for any other specific person who purchased 1 ticket in each lottery.

But the probability of someone, somewhere winning two lotteries in 4 months is a different matter altogether. Professors Diaconis and Mosteller (1989) calculated the chance of this happening to be only 1 in 30.

The citation for the original Diaconis and Mosteller article is:

Diaconis, P., & Mosteller., F. (1989). Methods for studying coincidences. Journal of the American Statistical Association, 84, 853-861.

In fact, as the above-linked article about the South Carolina homer barrage notes, the five "dingers" merely tied the NCAA record (set in 1998), rather than breaking it.

What about the tennis match that I started this write-up with? I've gone on too long for a detailed statistical analysis, so I'll just note that Rafael Nadal came into the French Open final having won 59 straight matches on clay (the surface in the French), whereas his opponent Roger Federer had won 27 consecutive matches in major (Grand Slam) tournaments, capturing Wimbledon, the U.S. Open, and the Australian Open, before advancing to the finals in Paris (none of these three tournaments won by Federer are played on clay). Nadal beat Federer, and I'll leave you to read about it here.

Welcome to the relaunching of the Hot Hand in Sports website. After somewhat over four years with the old look, I thought something new was in order. This new format should also provide several advantages over the old one:

*The URL is now much simpler (be sure to notice, however, that it's thehothand.blogspot.com; "hothand" without the "the" will lead to another, unrelated site).

*Readers can now comment on my entries (I've put in some steps, however, in an attempt to prevent spam).

*Over the years, my write-ups have been shifting away from long, detailed analytic pieces to brief summaries, always with a link to an article about the sports performance in question, and sometimes with statistical analyses of my own. The format on this new hosting site should fit well with my trend toward succinctness.

Another nice thing is that Blogspot has now made it much easier than before to post visual images. Though perhaps not as frequently as before, I still occasionally may want to post charts, graphs, and the like.

In the coming days and weeks, I will be inserting links on this new page, attempting to preserve as much of the information on the old page as possible. If there's something on the old page that you don't see here, please don't hesitate to inquire by e-mail (via the link to my faculty webpage in the upper-right portion of the page).

***

One recent, substantive hot streak that I wanted to mention is that the Angels' Vladimir Guerrero got a hit in all three late-May games against the Texas Rangers, meaning that he has now gotten at least one hit in all 42 games he's ever played against them. To quote the headline I came up with and was using on my old site, "Texas Can't Be Glad to See Vlad." The teams now don't play each other again until August.